Is there a math concept that never made sense to you?
-
Is there a math concept that never made sense to you? Which one or ones do you wish someone would explain in new ways?
If none of these come close you can mention something as a comment.
-
myrmepropagandistreplied to myrmepropagandist last edited by
Yes I think fractions cause people as many problems as these other "more advanced" ideas. I've seen students in calc 2 who still had messy ideas about fractions. It's not trivial and just because we teach some of it to 5th graders doesn't mean everyone knows how they work.
-
@futurebird Before I read down the thread I didn’t know what ‘the derivitive’ even related to
 My father was an engineer, and obnoxious about Being Right, so I went into visual art where the criticism couldn’t follow.
My father was an engineer, and obnoxious about Being Right, so I went into visual art where the criticism couldn’t follow. After he died I went back to school for Comp Sci and had to study up to place out of the intro math class — I like math now, but have still never taken a class more advanced than Algebra II (back in 1977 that was)
-
Infrapink (he/his/him)replied to @jacquiharper last edited by
@jacquiharper @futurebird Recently I've been casually trying to get a handle on what basic calculus is actually doing.
The derivative is the slope of the graph of a function at a given point. People talk about "rates of change" and "tangents", but no, it's a slope.
-
Matthew Millerreplied to myrmepropagandist last edited by
I have a vivid memory of asking a lot of "why" questions about fractions to my 6th grade teacher, and her (with no malice) being completely unable to provide anything beyond "because, obviously".
-
myrmepropagandistreplied to Infrapink (he/his/him) last edited by
Exactly. A “rate of change” is a slope. 20miles/hour is a line with slope 20/1 because, for each 1 hour you go forward in the x-direction, your total total distance goes up by 20 miles in the y-direction.
A tangent is a straight line … again with a slope. So “the slope of a curve at a point” (curves being precisely those lines with non-consonant slopes) we use the tangent to define it in a way so that our straight-line idea of slope works.

-
@futurebird Why does math even work (or rather logic and reasoning in general)??? I'm usually able to satisfy my intuition about any specific math concept I need to know, but this question keeps bothering me.
-
When you say it “works” what do you mean by that? Can you give an example of “math working” ? what would it NOT working look like?
-
I remember a childhood conversation where someone insisted that math is universal and that 1+1 = 2 to aliens and extra-dimensional beings, etc., and I said that I can't imagine anything else, but that I might just be too dumb to get it.
That ended in the other person being mad at me (I mean, in a harmless short-term way).
But I still kinda think I was on to something there.
-
@futurebird @mcc @pesasa @vikxin @Wharrrrrrgarbl @Kichae @whknott @dwildstr
Math and logic seem to map well onto the observed “real world”, despite how hard the complexity of reality usually fights back against being divided up into simple boxes. Math works by being useful tool in predicting stuff. Also it doesn't seem disagree with itself all the time. How to rule out the existence of some alternative, completely alien math like @mattdm said? Could there be something that breaks our logic but still helps predict things, maybe better than what we have?
It's a vague feeling and I find it difficult to completely get rid of, mostly because it directly challenges the fundamental validity of the tools I otherwise would rely on to seek clarity. Like, am I even allowed to try to think rationally? If not, how can I proceed at all? How to “prove” something if you can't just assume that any rules hold? Would it be possible to find solid answers from some specific kind of unhinged ramblings?
However, I actually do have something that tastes like an answer. It just feels like it bypasses the problem.
I'd say that math is based on some self-sustaining stable things in our brains. Maybe “attractor” is a correct word here – math could be seen as a system of strong attractors. It consists of tiny rules or patterns that our brains find easiest to hold onto and reproduce. We learn them by repeatedly observing corresponding similar (but not exactly equivalent) stable phenomena in the nature. For example, we think that three stones today is still three stones tomorrow, unless someone removes one of them or adds another. But what if we realize later that one of the stones is actually made of foam? Our simple rules are so sticky and dear to us that we rather count that as subtraction, too (someone tricked us and swapped a stone when we weren't looking), or we say that there were only two stones from the beginning, but we just didn't notice that one of them wasn't real. We would firmly refuse the conclusion that three is sometimes equal to two.
Maybe this is more or less what most of you meant in your replies?
I think the answer basically says “wrong question” and then turns it around, pointing outwards: why are some things in the universe simple enough that they can be modeled by a minuscule brain? And my hunch on that is: matter couldn't organize into even simplest life if the local environment was too chaotic to present lots of simple patterns.
Maybe practically satisfying, but not philosophically/mathematically or however it should be described.
-
To paraphrase a famous person: the basic rules of math are so obvious, that only a fool would doubt them. They are so universal (like 3 stones will always be 3 stones), that we would not be able to process, what we see, hear, etc., if they would turn out, not to be true.
And the rest can all be created from those basic rules by logic deduction. So they have to be true, if the basic rules are true.@futurebird @mcc @pesasa @vikxin @Wharrrrrrgarbl @Kichae @whknott @dwildstr @mattdm
-
@xilebo @nen @futurebird @mcc @pesasa @vikxin @Wharrrrrrgarbl @Kichae @whknott @dwildstr
Lots of things seem that way, but turn out to be more complicated. Maybe we just can't envision it with our puny three-dimensional organic primate brains.
-
@futurebird @Infrapink @jacquiharper
20mph isn't a rate of change; it's a velocity, unchanging.
32 feet per second squared is a rate of change, an accelearation.
A tangent is not a straight line.
-
@phaedral @futurebird @Infrapink @jacquiharper
A tangent is a straight line that touches a curve on exactly one point. The slope of that tangent is then considered the slope of the curve at that exact point. -
@dendari @futurebird @Infrapink @jacquiharper Arguably that's a different use of the word. Of course it's been 30+ years since second semester calculus, which is as far as I got.
"tangent" is defined:
Given an angle θ (in either degrees or radians) and the (x,y) coordinates of the corresponding point on the unit circle, we define tangent as
tan(θ)=y/x
Resulting in this curve:
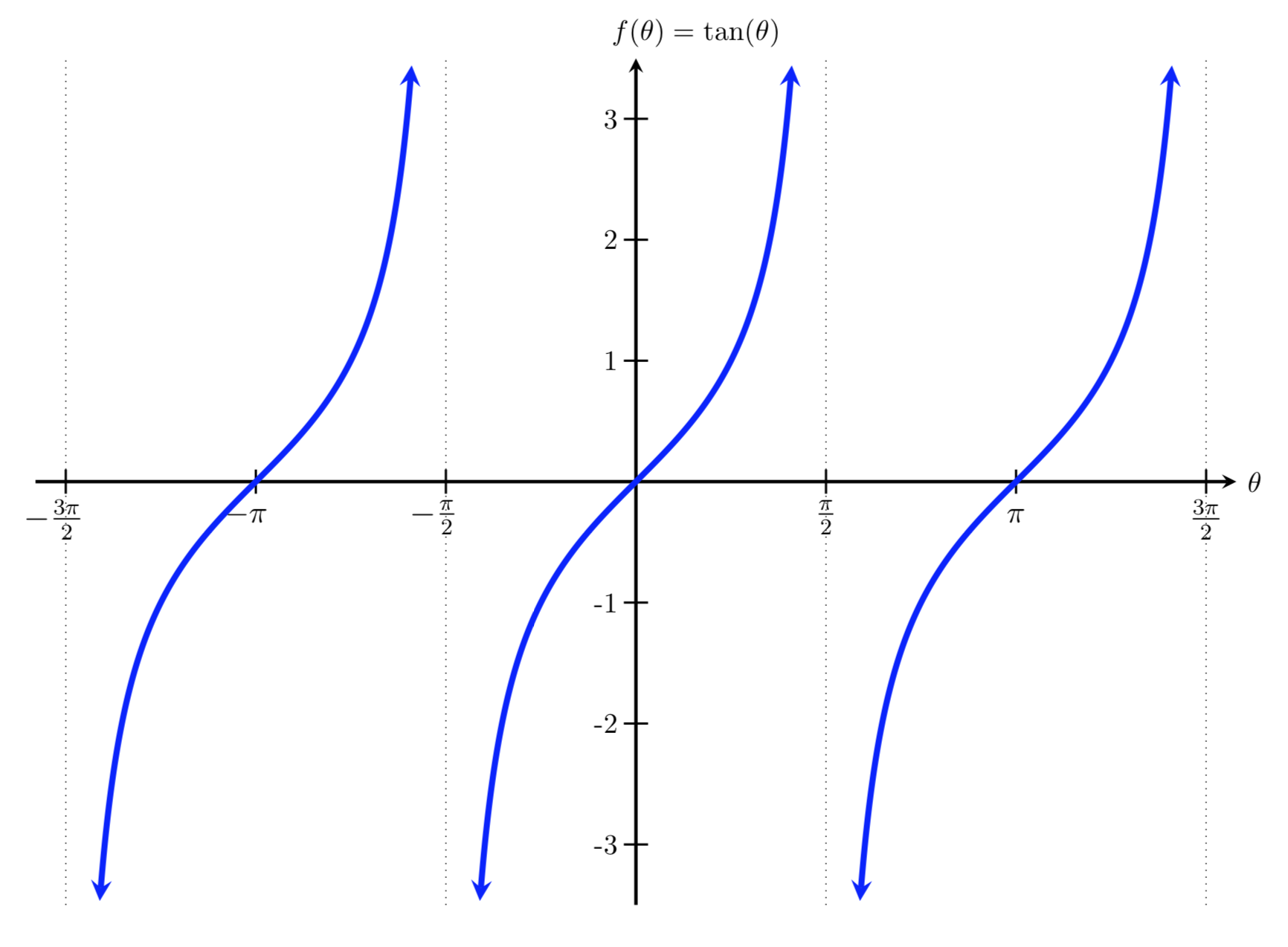
-
@phaedral @futurebird @Infrapink @jacquiharper this is the tangent from trigonometry not the same tangent.
Futurebird is likely a much better math teacher than I am. I haven't done anything beyond 8th grade algebra in years. -
@dendari @phaedral @Infrapink @jacquiharper
The crazy thing is... in a way it *is* the same tangent, or at least for a circle.
Most people know that you can plot a circle using:
x=cos theta
y=sin thetaAnd let theta go from 0 to 2pi (or 0 to 360 if you like)
Because the x and y co-ordinates of a circle are parametrized by the sin and cos.
Tangent has a geometric meaning here too. And this is why it increases without bound as theta gets close to pi/4 (90 degrees)
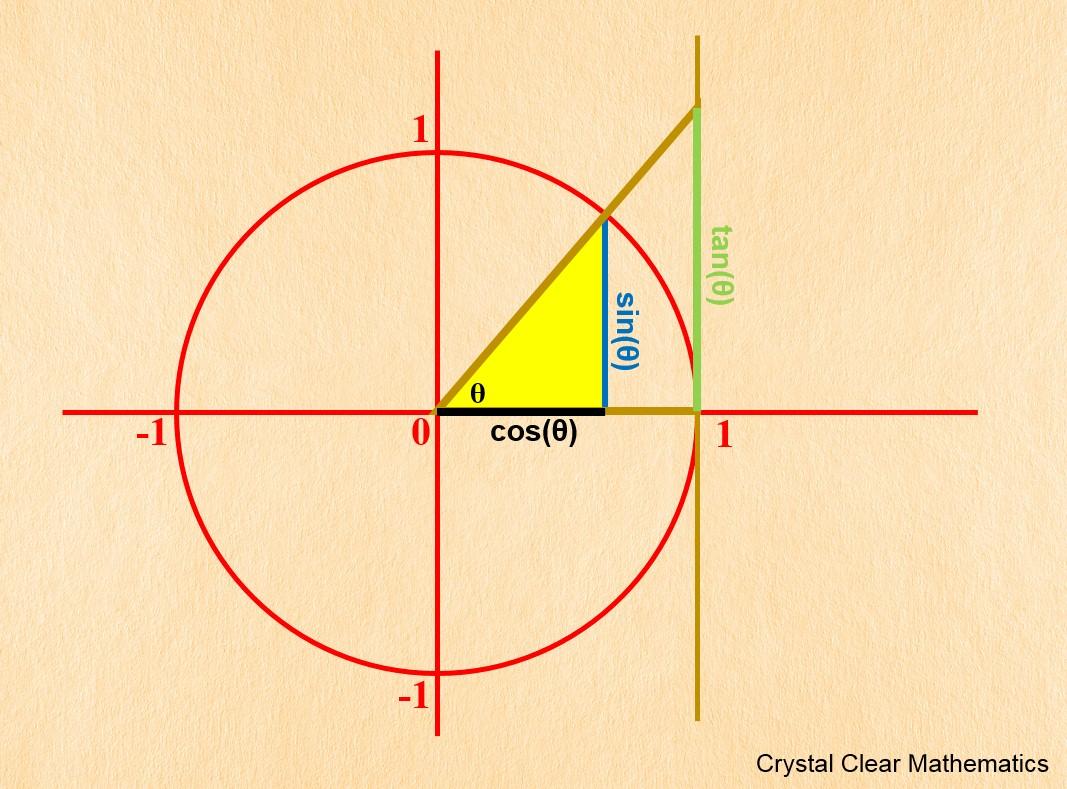
-
Matthew Millerreplied to myrmepropagandist last edited by
> Most people know that you can plot a circle using [...]
*cough*
-
@futurebird euler's identity blows my mind every single time. like, here we are chatting about natural logs all nice and casual then someone mentions pi and it's like ok so then what happens? some wise-ass throws in a an imaginary number and all of a sudden we are are at negative one. wtf? 🤯
-
I like Euler's identity. But it's also just sort of saying "cos(180 degrees) = -1"


