Is there a math concept that never made sense to you?
-
@xilebo @nen @futurebird @mcc @pesasa @vikxin @Wharrrrrrgarbl @Kichae @whknott @dwildstr
Lots of things seem that way, but turn out to be more complicated. Maybe we just can't envision it with our puny three-dimensional organic primate brains.
-
@futurebird @Infrapink @jacquiharper
20mph isn't a rate of change; it's a velocity, unchanging.
32 feet per second squared is a rate of change, an accelearation.
A tangent is not a straight line.
-
@phaedral @futurebird @Infrapink @jacquiharper
A tangent is a straight line that touches a curve on exactly one point. The slope of that tangent is then considered the slope of the curve at that exact point. -
@dendari @futurebird @Infrapink @jacquiharper Arguably that's a different use of the word. Of course it's been 30+ years since second semester calculus, which is as far as I got.
"tangent" is defined:
Given an angle θ (in either degrees or radians) and the (x,y) coordinates of the corresponding point on the unit circle, we define tangent as
tan(θ)=y/x
Resulting in this curve:

-
@phaedral @futurebird @Infrapink @jacquiharper this is the tangent from trigonometry not the same tangent.
Futurebird is likely a much better math teacher than I am. I haven't done anything beyond 8th grade algebra in years. -
@dendari @phaedral @Infrapink @jacquiharper
The crazy thing is... in a way it *is* the same tangent, or at least for a circle.
Most people know that you can plot a circle using:
x=cos theta
y=sin thetaAnd let theta go from 0 to 2pi (or 0 to 360 if you like)
Because the x and y co-ordinates of a circle are parametrized by the sin and cos.
Tangent has a geometric meaning here too. And this is why it increases without bound as theta gets close to pi/4 (90 degrees)
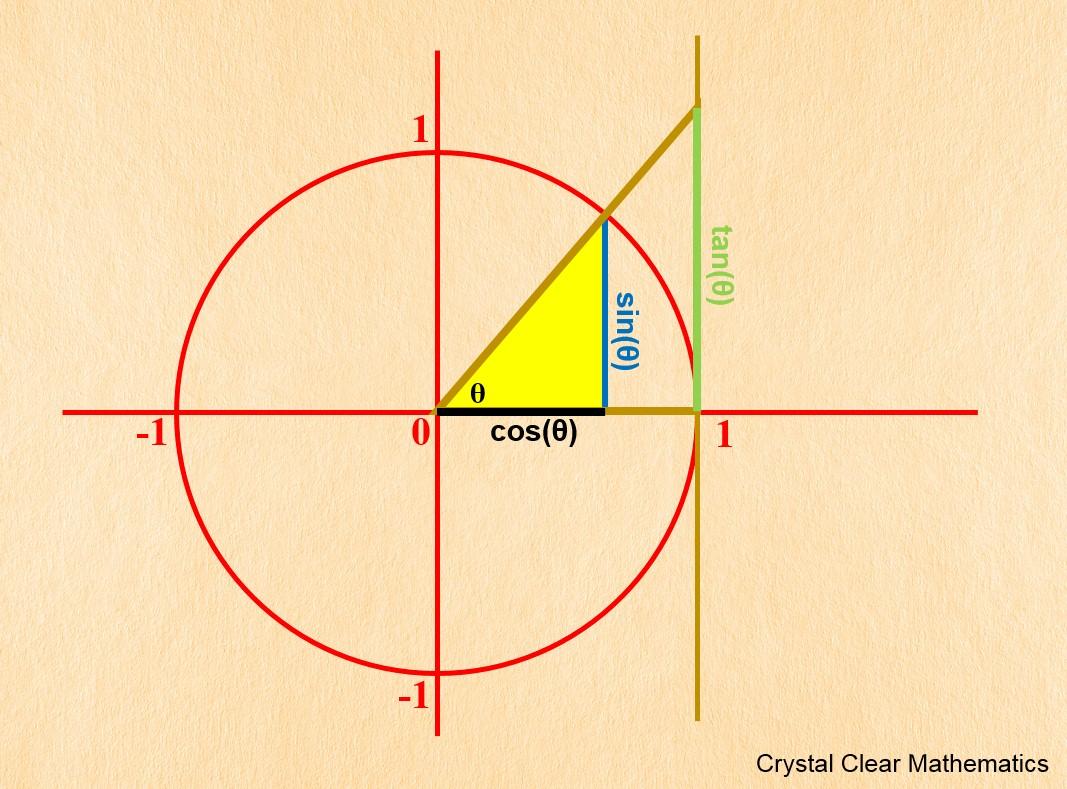
-
Matthew Millerreplied to myrmepropagandist last edited by
> Most people know that you can plot a circle using [...]
*cough*
-
@futurebird euler's identity blows my mind every single time. like, here we are chatting about natural logs all nice and casual then someone mentions pi and it's like ok so then what happens? some wise-ass throws in a an imaginary number and all of a sudden we are are at negative one. wtf? 🤯
-
I like Euler's identity. But it's also just sort of saying "cos(180 degrees) = -1"
-
@futurebird @keithpjolley
Yeah, the truly surprising part of Euler's identity isn't that; it's “exponentiation is a sprial.”


